이진 트리는 노드들이 최대 2개의 자식 노드를 가지는 트리를 말합니다.
이러한 이진 트리를 순회하는 방법에는 전위 순회, 중위 순회, 후위 순회가 있습니다.
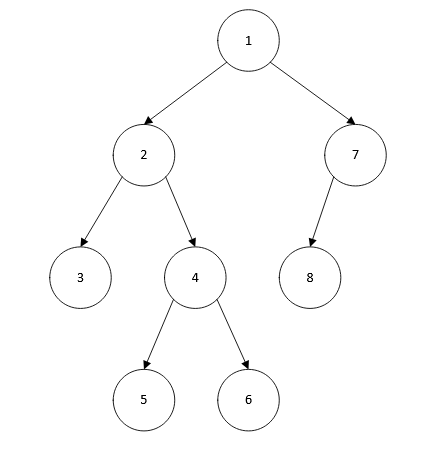
전위 순회 (Pre-order traversal) : 루트 노드부터 시작하여, 루트를 방문하고 왼쪽 서브 트리를 순회하고, 오른쪽 서브 트리를 순회합니다. 순서는 루트 -> 왼쪽 -> 오른쪽입니다. (예시: 1 -> 2 -> 3 -> 4 -> 5 -> 6 -> 7 -> 8)
중위 순회 (In-order traversal) : 왼쪽 서브 트리부터 시작하여, 왼쪽 서브 트리를 순회하고, 루트를 방문하고, 오른쪽 서브 트리를 순회합니다. 순서는 왼쪽 -> 루트 -> 오른쪽입니다. (예시: 3 -> 2 -> 5 -> 4 -> 6 -> 1 -> 8 -> 7)
후위 순회 (Post-order traversal) : 왼쪽 서브 트리부터 시작하여, 왼쪽 서브 트리를 순회하고, 오른쪽 서브 트리를 순회하고, 루트를 방문합니다. 순서는 왼쪽 -> 오른쪽 -> 루트입니다. (예시: 3 -> 5 -> 6 -> 4 -> 2 -> 8 -> 7 -> 1)
이진 트리는 특성상 재귀함수를 사용하면 순회들을 구현하기 간단합니다.
다음은 Python에서의 구현입니다.
class Node:
def __init__(self, value: int, left=None, right=None):
self.value = value
self.left = left
self.right = right
def pre_order(node: Node) -> None:
print(node.value, end=" ")
if node.left:
pre_order(node.left)
if node.right:
pre_order(node.right)
return None
def in_order(node: Node) -> None:
if node.left:
in_order(node.left)
print(node.value, end=" ")
if node.right:
in_order(node.right)
return None
def post_order(node: Node) -> None:
if node.left:
post_order(node.left)
if node.right:
post_order(node.right)
print(node.value, end=" ")
return None
tree_init = Node(1, Node(2, Node(3), Node(4, Node(5), Node(6))), Node(7, Node(8)))
pre_order(tree_init)
print()
in_order(tree_init)
print()
post_order(tree_init)
# Output
# 1 2 3 4 5 6 7 8
# 3 2 5 4 6 1 8 7
# 3 5 6 4 2 8 7 1입력은 위의 예시와 동일한 것을 사용했고, 보시다시피 예시와 동일한 결과를 보여줍니다.
